MONOCORDO
MONOCORDO – Strumento a corda unica
Il Monocordo è uno strumento inventato (secondo Boezio) da Pitagora (570 a.C – matematico e filosofo Greco). Composto da un’unica corda (per esempio della lunghezza di sessanta centimetri) posizionata su di una cassa di risonanza tra due ponticelli fissi, al di sotto della quale scorre indipendente un capotasto o ponticello mobile (chiamato anche cavaliere), che la divide in due parti di lunghezza modificabile. La corda pizzicata senza il capotasto (corda libera) restituisce una nota detta fondamentale.
Dapprima Pitagora divise la corda in due parti posizionando il capotasto esattamente a metà. Pizzicando poi la parte destra scoprì che restituiva lo stesso suono della nota fondamentale ma ad un’altezza diversa, ovvero all’ottava superiore (rapporto 2:1). Pitagora decise poi di dividere la corda in tre parti (rapporto 3:2) ottenendo così un suono differente (intervallo di 5ª). Questa lunghezza di fatto produce un suono che ben si sposa con quello prodotto dalla corda intera e ciò è dovuto alla consonanza (l’insieme dei due suoni risulta gradevole all’orecchio). Dividendo ulteriormente la corda in quattro parti (rapporto 4:3) ottenne poi l’intervallo di 4ª. . .
1/1 Unisono – 2/1 Ottava – 3/2 Quinta – 4/3 Quarta
Rapporto Lunghezze
1:2
2:3
3:4
Rapporto Frequenze
2:1
3:2
4:3
Intervallo Consonante
Ottava
Quinta
Quarta
Pitagora scoprì quindi che le altezze delle note musicali ottenute pizzicando le corde dipendevano esclusivamente dalle loro lunghezze. Inoltre, egli scoprì che le altezze sono fra di loro collegate da Numeri Razionali. Grazie al Monocordo, i pitagorici studiarono le consonanze fra i suoni e capirono che era possibile ottenere un suono consonante solo quando le lunghezze delle due parti della corda divisa dal capotasto, erano rappresentate da rapporti di numeri interi piccoli.
****La consonanza si ha quando due o più note suonate simultaneamente restituiscono una sensazione di stabilità, omogeneità o come la definiva Pitagora gradevolezza**** mentre la dissonanza crea una sensazione di instabilità, per Pitagora essa era fastidiosa. Chiaramente la musica moderna è ricchissima di dissonanze e questa definizione data al tempo non è più valida al giorno d’oggi.
La consonanza si perde quando il rapporto dei due numeri (piccoli) si alza. Osservando la scala pitagorica è possibile notare che negli intervalli Do/Mi = 81/64 – Do/La = 27/16 e Do/Si = 243/128 il rapporto di frequenza non è più composto da piccoli numeri e quindi tutt‘altro che consonanti.
Pitagora aveva un’adorazione per il ***numero 10 – 1+2+3+4 = 10 – considerato numero magico dai Pitagorici (Tetraktys)***. Questo è uno dei motivi per il quale egli non considerò i rapporti di 5/4 (Do–Mi terza maggiore), 5/3 (Do–La sesta maggiore) e 6/5 (Re–Fa terza minore), i quali si possono ancora considerare a tutti gli effetti suoni consonanti. Egli compose la scala senza questi rapporti, utilizzando solo i numeri 1 – 2 – 3 – 4 e facendo delle trasposizioni di ottava per ritornare all’ottava di partenza, ottenendo però delle terze, seste e settime insoddisfacenti.
La scala pitagorica era perfetta per la musica monodica greca, ma con la nascita della polifonia ai tempi del Medioevo, alcuni intervalli risultarono poco piacevoli all’orecchio e si sentì così l’esigenza di una nuova scala. . .

****La consonanza non riguarda solo i suoni simultanei (intervallo armonico) ma anche i suoni consecutivi (intervallo melodico)****
***Nella scala pitagorica – utilizzata per duemila anni – vi sono solo i numeri 1 – 2 – 3 – 4 ed era l’unica scala ammessa dalla Chiesa Cattolica nella musica liturgica***
Inoltre Pitagora amava il quadrato magico (anche se questo è in realtà una sorta di pseudo-quadrato magico, in quanto ha dei numeri che si ripetono), all’interno del quale sommando i numeri in tutte le direzioni (linee – colonne e diagonali) il risultato che restituisce è sempre 10.
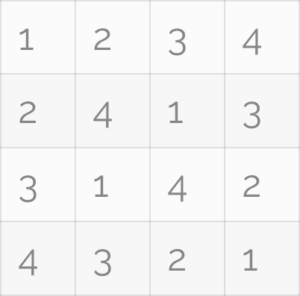
***E’ anche vero però, che Pitagora disse che proprio il numero 5 rappresentava l’armonia, in quanto si otteneva dal 3+2. Inoltre, il pentagono stellato era uno dei simboli della scuola pitagorica, mentre l’unione tra il primo numero pari, femminile (ovvero il 2) e il primo numero dispari, maschile (ovvero il 3), da come risultato proprio il numero 5. I pitagorici collegavano il 5 all’amore e al matrimonio***
N.B. Pitagora non poteva supporre né immaginare il legame tra l’altezza di un suono e la sua frequenza. Egli realizzò che più la corda è lunga, più la nota è grave. Viceversa, più la corda è corta più la nota è acuta. Il filosofo di Samo successivamente collegò un numero ad ogni nota, per esempio: il suono emesso da una corda di dimensione pari ad un metro di lunghezza l’associò al numero 1, mentre la nota prodotta da una corda lunga mezzo metro l’associò al numero 2, etc.
DA CHE COSA DIPENDE LA FREQUENZA?
- Lunghezza della corda: la frequenza è inversamente proporzionale ad essa; maggiore è la lunghezza, minore è la frequenza (suono meno acuto).
- Tensione della corda: la frequenza dipende in maniera proporzionale ad essa; maggiore è il livello di tensione, maggiore è la frequenza di vibrazione (suono più acuto).
- Diametro della corda: la frequenza dipende in modo inversamente proporzionale ad esso; maggiore è il diametro, minore è la frequenza (suono meno acuto).
- Densità lineare della corda: la frequenza dipende in modo inversamente proporzionale ad essa; maggiore è la densità lineare, minore è la frequenza (suono meno acuto).
La densità lineare rappresenta la massa o quantità di materia contenuta in un’unità di lunghezza. La frequenza di vibrazione è inversamente proporzionale alla densità lineare della corda, ciò significa che utilizzando una corda più sottile (quindi con una densità lineare minore), la frequenza aumenta e utilizzando una corda più spessa (quindi con una densità lineare maggiore), la frequenza diminuisce.
Esempio di calcolo della densità lineare di una corda:
Supponiamo di avere una corda pari alla lunghezza di 1 metro con una massa pari a 100 grammi. Per calcolare la densità lineare della corda, dobbiamo dividere la massa per la sua lunghezza:
Densità lineare = massa / lunghezza
Densità lineare = 100 g / 1 m
Densità lineare = 100 g/m
Quindi, la densità lineare (in questo caso) è pari a 100 grammi per metro. Questo significa che ogni metro di corda ha una massa di 100 grammi.
N.B. Il diametro e la densità lineare sono grandezze fisiche correlate tra di loro. Infatti, il diametro di una corda influisce sulla sua densità lineare e viceversa. In generale, se il diametro della corda aumenta, anche la sua densità lineare aumenta, poiché la corda ha più materia per unità di lunghezza. Al contrario, se il diametro della corda diminuisce, anche la sua densità lineare diminuisce, poiché c’è meno materia per unità di lunghezza. Ad ogni modo, ci possono essere eccezioni a questa regola, a seconda delle proprietà specifiche del materiale utilizzato per la corda.
LEGGE DI MERSENNE
COSTRUIAMO IL MONOCORDO PITAGORICO – Raffaello Scuola
Clicca sul titolo per visionare il PDF
Pitagora credeva che l’universo fosse una sorta di monocordo sconfinato, con la sua unica corda tesa tra cielo e terra. L’estremità superiore della corda era connessa allo spirito assoluto, mentre l’estremità inferiore alla materia assoluta.
A cura di Serena Giannini
MONOCORDO – Strumento a corda unica
Il Monocordo è uno strumento inventato (secondo Boezio) da Pitagora (570 a.C – matematico e filosofo Greco). Composto da un’unica corda (per esempio della lunghezza di sessanta centimetri) posizionata su di una cassa di risonanza tra due ponticelli fissi, al di sotto della quale scorre indipendente un capotasto o ponticello mobile (chiamato anche cavaliere), che la divide in due parti di lunghezza modificabile. La corda pizzicata senza il capotasto (corda libera) restituisce una nota detta fondamentale.
Dapprima Pitagora divise la corda in due parti posizionando il capotasto esattamente a metà. Pizzicando poi la parte destra scoprì che restituiva lo stesso suono della nota fondamentale ma ad un’altezza diversa, ovvero all’ottava superiore (rapporto 2:1). Pitagora decise poi di dividere la corda in tre parti (rapporto 3:2) ottenendo così un suono differente (intervallo di 5ª). Questa lunghezza di fatto produce un suono che ben si sposa con quello prodotto dalla corda intera e ciò è dovuto alla consonanza (l’insieme dei due suoni risulta gradevole all’orecchio). Dividendo ulteriormente la corda in quattro parti (rapporto 4:3) ottenne poi l’intervallo di 4ª. . .
1/1 Unisono – 2/1 Ottava – 3/2 Quinta – 4/3 Quarta
Rapporto Rapporto Intervallo Lunghezze Frequenze Consonante 1:2 2:1 Ottava 2:3 3:2 Quinta 3:4 4:3 Quarta
Pitagora scoprì quindi che le altezze delle note musicali ottenute pizzicando le corde dipendevano esclusivamente dalle loro lunghezze. Inoltre, egli scoprì che le altezze sono fra di loro collegate da Numeri Razionali. Grazie al Monocordo, i pitagorici studiarono le consonanze fra i suoni e capirono che era possibile ottenere un suono consonante solo quando le lunghezze delle due parti della corda divisa dal capotasto, erano rappresentate da rapporti di numeri interi piccoli.
****La consonanza si ha quando due o più note suonate simultaneamente restituiscono una sensazione di stabilità, omogeneità o come la definiva Pitagora gradevolezza**** mentre la dissonanza crea una sensazione di instabilità, per Pitagora essa era fastidiosa. Chiaramente la musica moderna è ricchissima di dissonanze e questa definizione data al tempo non è più valida al giorno d’oggi.
La consonanza si perde quando il rapporto dei due numeri (piccoli) si alza. Osservando la scala pitagorica è possibile notare che negli intervalli Do/Mi = 81/64 – Do/La = 27/16 e Do/Si = 243/128 il rapporto di frequenza non è più composto da piccoli numeri e quindi tutt‘altro che consonanti.
Pitagora aveva un’adorazione per il ***numero 10 – 1+2+3+4 = 10 – considerato numero magico dai Pitagorici (Tetraktys)***. Questo è uno dei motivi per il quale egli non considerò i rapporti di 5/4 (Do–Mi terza maggiore), 5/3 (Do–La sesta maggiore) e 6/5 (Re–Fa terza minore), i quali si possono ancora considerare a tutti gli effetti suoni consonanti. Egli compose la scala senza questi rapporti, utilizzando solo i numeri 1 – 2 – 3 – 4 e facendo delle trasposizioni di ottava per ritornare all’ottava di partenza, ottenendo però delle terze, seste e settime insoddisfacenti.
La scala pitagorica era perfetta per la musica monodica greca, ma con la nascita della polifonia ai tempi del Medioevo, alcuni intervalli risultarono poco piacevoli all’orecchio e si sentì così l’esigenza di una nuova scala. . .

****La consonanza non riguarda solo i suoni simultanei (intervallo armonico) ma anche i suoni consecutivi (intervallo melodico)****
***Nella scala pitagorica – utilizzata per duemila anni – vi sono solo i numeri 1 – 2 – 3 – 4 ed era l’unica scala ammessa dalla Chiesa Cattolica nella musica liturgica***
Inoltre Pitagora amava il quadrato magico (anche se questo è in realtà una sorta di pseudo-quadrato magico, in quanto ha dei numeri che si ripetono), all’interno del quale sommando i numeri in tutte le direzioni (linee – colonne e diagonali) il risultato che restituisce è sempre 10.

***E’ anche vero però, che Pitagora disse che proprio il numero 5 rappresentava l’armonia, in quanto si otteneva dal 3+2. Inoltre, il pentagono stellato era uno dei simboli della scuola pitagorica, mentre l’unione tra il primo numero pari, femminile (ovvero il 2) e il primo numero dispari, maschile (ovvero il 3), da come risultato proprio il numero 5. I pitagorici collegavano il 5 all’amore e al matrimonio***
N.B. Pitagora non poteva supporre né immaginare il legame tra l’altezza di un suono e la sua frequenza. Egli realizzò che più la corda è lunga, più la nota è grave. Viceversa, più la corda è corta più la nota è acuta. Il filosofo di Samo successivamente collegò un numero ad ogni nota, per esempio: il suono emesso da una corda di dimensione pari ad un metro di lunghezza l’associò al numero 1, mentre la nota prodotta da una corda lunga mezzo metro l’associò al numero 2, etc.
DA CHE COSA DIPENDE LA FREQUENZA?
- Lunghezza della corda: la frequenza è inversamente proporzionale ad essa; maggiore è la lunghezza, minore è la frequenza (suono meno acuto).
- Tensione della corda: la frequenza dipende in maniera proporzionale ad essa; maggiore è il livello di tensione, maggiore è la frequenza di vibrazione (suono più acuto).
- Diametro della corda: la frequenza dipende in modo inversamente proporzionale ad esso; maggiore è il diametro, minore è la frequenza (suono meno acuto).
- Densità lineare della corda: la frequenza dipende in modo inversamente proporzionale ad essa; maggiore è la densità lineare, minore è la frequenza (suono meno acuto).
La densità lineare rappresenta la massa o quantità di materia contenuta in un’unità di lunghezza. La frequenza di vibrazione è inversamente proporzionale alla densità lineare della corda, ciò significa che utilizzando una corda più sottile (quindi con una densità lineare minore), la frequenza aumenta e utilizzando una corda più spessa (quindi con una densità lineare maggiore), la frequenza diminuisce.
Esempio di calcolo della densità lineare di una corda:
Supponiamo di avere una corda pari alla lunghezza di 1 metro con una massa pari a 100 grammi. Per calcolare la densità lineare della corda, dobbiamo dividere la massa per la sua lunghezza:
Densità lineare = massa / lunghezza
Densità lineare = 100 g / 1 m
Densità lineare = 100 g/m
Quindi, la densità lineare (in questo caso) è pari a 100 grammi per metro. Questo significa che ogni metro di corda ha una massa di 100 grammi.
N.B. Il diametro e la densità lineare sono grandezze fisiche correlate tra di loro. Infatti, il diametro di una corda influisce sulla sua densità lineare e viceversa. In generale, se il diametro della corda aumenta, anche la sua densità lineare aumenta, poiché la corda ha più materia per unità di lunghezza. Al contrario, se il diametro della corda diminuisce, anche la sua densità lineare diminuisce, poiché c’è meno materia per unità di lunghezza. Ad ogni modo, ci possono essere eccezioni a questa regola, a seconda delle proprietà specifiche del materiale utilizzato per la corda.
LEGGE DI MERSENNE
COSTRUIAMO IL MONOCORDO PITAGORICO – Raffaello Scuola
Clicca sul titolo per visionare il PDF





















No Comments